
牛顿没解决的问题,AI给你解决了?
AI的推理能力一直是研究的焦点。作为最纯粹、要求最高的推理形式之一,能否解决高级的数学问题,无疑是衡量语言模型推理水平的一把尺。
虽然我们已经见证过来自谷歌DeepMind的Al以一分之差痛失IMO金牌,也从陶哲轩频频更新的动态中得知,AI工具已经在帮助数学家解决像「纽结理论」和「海狸难题」这样困扰数学家几个世纪的难题。
但是这些成果大多数都需要数学家作大量的前期工作,对于没有已知通用解法的开放性问题,AI也是一个小白。

最近的一项研究打破了这个局面。Meta和巴黎理工学院的研究人员共同探讨了一个困扰数学界长达132年的问题:李雅普诺夫函数。简单来说,李雅普诺夫函数用于判断一个动力系统相对于其平衡点或轨道,随着时间无限延长后是否能保持全局稳定。论文已经入选了NeurIPS 2024。

论文标题:Global Lyapunov functions: a long-standing open problem in mathematics, with symbolic transformers
论文地址:https://arxiv.org/pdf/2410.08304
这类问题中,最出名的可能就是三体问题了:两个物体在没有其他引力的影响下相互绕行,如果再添加一个物体,在大多数情况下,这三个物体的运动都会变得混乱起来。
牛顿、拉格朗日和庞加莱都研究三体问题,但都没有找到根本性的解决方案。著名俄罗斯数学家和物理学家李雅普诺夫(Александр Ляпунов)发现,如果能找到系统的类熵函数—李雅普诺夫函数,就能保证系统的稳定性。遗憾的是,目前还没有已知的方法来推导一般情况下的李雅普诺夫函数,而且只发现了极少系统的李雅普诺夫函数解。
在最新的这项研究中,研究者提出了一种从随机采样的李雅普诺夫函数生成训练数据的新技术。在这些数据集上训练的序列到序列Transformer在held-out测试集上达到了近乎完美的准确率(99%),在分布外测试集上达到了非常高的性能(73%)。
这项研究表明,通过使用少量(300 个)可以用现有算法方法解决的简单样本来丰富训练集,可以获得更高的准确率(84%)。AI模型在各种基准测试中的表现已经远超最先进的技术和人类的表现。
研究者表示,生成模型可用于解决数学研究层面的问题,为数学家提供可能解决方案的猜测。黑箱模型提出的解决方案是明确的,其数学正确性可以得到验证。或许,这项研究是解决数学开放问题的人工智能驱动蓝图。
三体问题与李雅普诺夫函数
三体问题是经典力学中最著名的未解问题之一。牛顿提出了万有引力定律,并通过微积分为两个物体之间的引力相互作用提供了精确的解。然而,当系统中增加第三个物体时,系统的复杂性显著增加,传统方法无法应对。

18世纪,拉格朗日做出了突破性的贡献:拉格朗日点。三体系统将在拉格朗日点达到平衡。然而,他的发现依然无法解决三体系统在长时间尺度下的整体稳定性问题。
到了19世纪末,庞加莱通过发展拓扑学和混沌理论,证明了某些条件下,三体系统会出现不可预测的混沌行为。这表明三体问题的复杂程度远超人们的想象,也意味着不存在普适的解。
1892年,李雅普诺夫又将这个世纪难题向前推进了一步。判断三体系统是否稳定,可以借助李雅普诺夫函数。
李雅普诺夫函数 V(x)需要满足以下条件才能保证系统的稳定性:
1.稳定平衡点
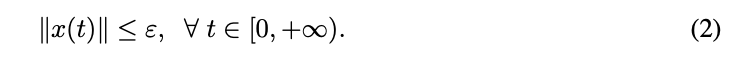
2.全域渐近稳定平衡点
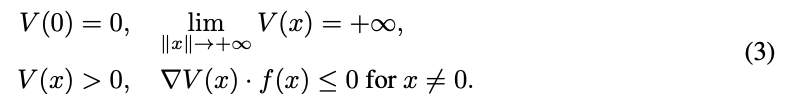
不过,李雅普诺夫只提供了理论上的证明,想要实际计算出一个系统的函数解极为困难。虽然像 SOSTOOLS 这样的计算工具可以辅助,但它们的能力仅限于处理小型的多项式系统,对于更复杂的情况往往无能为力。
这项工作中,研究者训练序列到序列 Transformer 来预测给定系统的 Lyapunov 函数。他们将这个问题定义为一个翻译任务:问题和解决方案以符号Token序列的形式表示,模型从生成的系统和 Lyapunov 函数对中训练,以最小化预测序列和正确解决方案之间的交叉熵。研究者使用学习率为 10^-4 的 Adam 优化器,在 16 个样本的批上训练具有 8 层、10 个注意力头和 640 嵌入维度的 Transformer,初始线性热身阶段为 10000 个优化步骤,并进行反平方根调度。所有实验都在 8 个 V100 GPU 和 32 GB 内存上运行,每个 GPU 的训练时间为 12 到 15 个小时。
数据生成
本文模型是在成对稳定系统和相关 Lyapunov 函数的大型数据集上进行训练和测试的。对此类稳定系统进行采样会遇到两个难题:首先,大多数动态系统都是不稳定的,没有通用的方法来判断一个系统是否稳定;其次,一旦对稳定系统进行采样,除了特殊情况外,没有找到 Lyapunov 函数的通用技术。
对于一般情况,研究者这里采用了后向生成法 ,即采样求解并生成相关问题;而对于小程度的可控多项式系统,研究者采用前向生成法,即采样系统并用求解器计算其解。
研究者生成了 2 个后向数据集和 2 个前向数据集用于训练和评估,并生成了一个较小的前向数据集用于评估。
后向数据集 BPoly 包含 100 万个非退化多项式系统 S,其系数为整数,等式数为 2 到 5(比例相同)。研究者还创建了 BNonPoly,一个包含 100 万个非退化非多项式系统、2 至 5 个等式的数据集。在这个数据集中,f 的坐标是通用函数的多项式,对于这类系统,目前还没有发现 Lyapunov 函数的方法。
两个前向数据集都是使用 Python 的 SumOfSquares 软件包中的求解器生成的,并采用了与 SOSTOOLS 类似的技术。这些数据集中的所有系统都是具有 2 到 3 个方程的非零整数多项式和整数多项式 Lyapunov 函数,这些方法只能求解这些系统。FLyap是一个包含 10 万个系统的数据集,这些系统的 Lyapunov 函数都是非同次多项式;FBarr 是一个有 30 万个以非均质多项式作为障碍函数的系统。这些数据集规模较小的原因在于 SOS 方法的计算成本以及发现 Lyapunov 或障碍函数的难度。
为了与发现多项式系统 Lyapunov 函数的最先进方法 SOSTOOL 进行比较,研究者还生成了一个测试集,其中包含 SOSTOOLS 可以求解的 1500 个具有整数系数的多项式系统(FSOSTOOLS)。
结果
研究者在不同数据集上训练的模型,在held-out测试集上达到了近乎完美的准确性,且在分布外测试集上则有非常高的性能,尤其是在用少量前向样本丰富训练集时。这些模型的性能大大优于此前最先进的技术,而且还能发现新系统的 Lyapunov 函数。
分布内/分布外准确率
表2展示了 4 个数据集上训练的模型性能。在它们所训练的数据集的保留测试集上进行测试时,所有模型都达到了很高的域内准确率。在前向数据集上,障碍函数的预测准确率超过 90%,Lyapunov 函数的预测准确率超过 80%。在后向数据集上,基于 BPoly 训练的模型的准确率接近 100%。可以注意到,集束搜索,即允许对解法进行多次猜测,能显著提高性能(对于性能较低的模型,束大小为 50 时,性能提高 7% 至 10%)。研究者在所有进一步的实验中都使用了束大小 50。

检验在生成数据上训练模型的试金石是它们在分布外(OOD)的泛化能力。表 3 展示了后向模型在前向生成集上的评估结果。在使用平方和 Lyapunov 函数(FLyap)对前向生成的随机多项式系统进行测试时,所有后向模型都达到了很高的准确率(73% 到 75%)。非多项式系统(BNonPoly)是最多样化的训练集,其性能也最好。在前向生成的具有障碍函数(FBarr)的系统集上,后向模型的精度较低,这可能是由于许多障碍函数并不一定是 Lyapunov 函数。在这些测试集上,后向模型必须应对不同的分布和(略微)不同的任务。另一方面,前向模型在后向测试集上的性能较低。这可能是由于这些训练集的规模较小。

总的来说,这些结果似乎证实了后向训练模型并没有学会反转其生成过程。如果是这样的话,它们在前向测试集上的表现就会接近于零。
丰富训练分布以提高性能
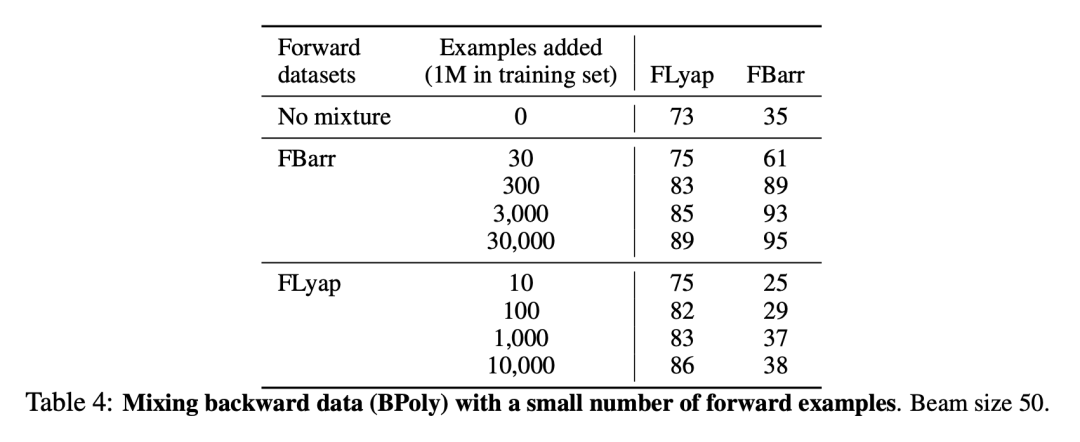
为了提高后向模型的 OOD 性能,研究者在其训练集中加入了极少量的前向生成的样本,带来了性能的显著提高,如表4所示。将 FBarr 中的 300 个样本添加到 BPoly 中,FBarr 的准确率从 35% 提高到 89%(尽管训练集中前向样本的比例仅为 0.03%),而 FLyap 的 OOD 准确率提高了 10 个百分点以上。增加 FLyap 中的样本带来的改进较小。这些结果表明,通过在训练集中添加少量(几十个或几百个)我们知道如何求解的样本,可以大大提高根据后向生成数据训练的模型的 OOD 性能。在这里,额外的样本解决了一个较弱但相关的问题:发现障碍函数。由于提高性能所需的样本数量很少,因此这种技术特别具有成本效益。
与baseline的对比
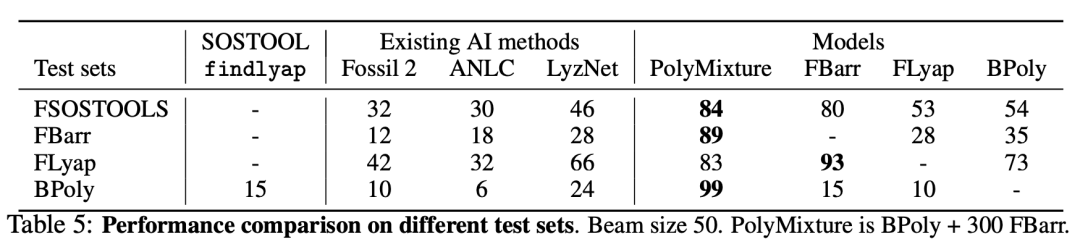
如表 5所示,在 FSOSTOOLS 上,一个以 BPoly 为基础并辅以 500 个 FBarr 系统训练的模型(PolyMixture)达到了 84%的准确率,证实了混合模型的高 OOD 准确率。在所有生成的测试集上,PolyMixture 的准确率都超过了 84%,而 findlyap 在后向生成的测试集上的准确率仅为 15%。这表明,在多项式系统上,与以前的技术水平相比,通过后向生成数据训练的Transformer取得了非常出色的结果。
平均而言,基于Transformer的模型也比 SOS 方法快得多。当尝试求解一个包含 2 至 5 个方程的随机多项式系统时,findlyap 平均需要 935.2 秒(超时 2400 秒)。对于本文模型,使用greedy decoding时,推理和验证一个系统平均需要 2.6 秒,使用束大小为 50 时需要 13.9 秒。
发现新数学
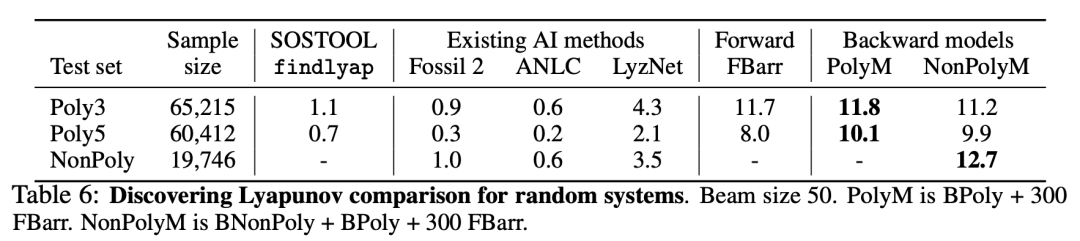
表 6 列出了本文模型发现的正确解的百分比。在多项式数据集上,最佳模型(PolyM)分别在 11.8%和 10.1%的(degree 3和degree 5)系统中发现了 Lyapunov 函数,是 findlyap 的 10 倍。对于非多项式系统,有 12.7% 的样本发现了 Lyapunov 函数。这些结果表明,从生成的系统数据集和 Lyapunov 函数中训练出来的语言模型确实可以发现未知的 Lyapunov 函数,其性能远远高于最先进的 SOS 求解器。
专家迭代
鉴于表 6 中模型的性能,可以利用新解决的问题来进一步微调模型。具体来说,研究者创建了一个针对多项式系统的经过验证的模型预测样本 FIntoTheWild,并将其添加到原始训练样本中,然后继续训练模型。他们还测试了对模型进行微调的不同策略,并在表 7 中总结了正向基准和「wild」的性能。
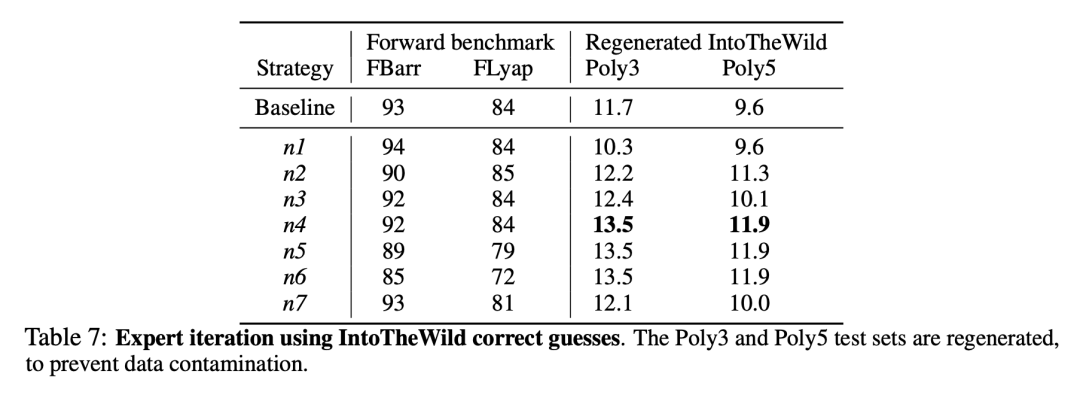
在 100 万个训练集的基础上增加 1000 个经过验证的预测后,「to into wild」测试集的性能提高了约 15%,而其他测试集(n4)的性能则没有受到影响。增加更多样本似乎是有害的,因为这会降低在其他基准(n5 和 n6)上的性能。研究者还注意到,使用来自其他分布的混合数据进行微调并不高效(结果 n1 和 n2),而使用少量数据已经有助于获得一些改进(结果 n3)。最后,使用来自 FIntoTheWild 的数据从头开始预训练模型并不高效(结果 n7)。
更多研究细节,可参考原论文。


 新浪科技公众号
新浪科技公众号 “掌”握科技鲜闻 (微信搜索techsina或扫描左侧二维码关注)
 相关新闻
相关新闻